If you have ever done any googling on memory and forgetting, you have probably encountered the concept of the forgetting curve. I have been doing some research on it as well and have noticed that most of the articles lack the detail that is available only in the scientific literature. So I read some scientific papers to really understand the topic and here is what I learned.
As a general rule, the forgetting curve tells us that in about 1 day you forget about 70 % of the information you have read or heard. The remaining 30% are forgotten at a slower rate – some studies show that in about 31 days you will remember only 4 % of what you have learned and others show this number to be about 20%.
It is important to remember that these percentages were derived by memorizing lists of nonsense syllables. The percentages might vary depending on numerous factors such as the type of information that is being memorized, the person who is learning the information, the conditions under which learning is being performed, etc.
Of course, these are just the general takeaways – if you dig a bit deeper into the topic you will learn that that the truth is a bit more nuanced. And to really understand what is the learning curve it is worth looking into how it was created in the first place. So buckle up because in this article we will explore the learning curve in depth!
The backstory of Hermann Ebbinghaus and the Forgetting Curve
Herman Ebbinghaus (1850-1909) was a German psychologist who was one of the first scientists to study our memory in an experimental way. His early studies and work on forgetting were published in 1885 in a book Über das Gedächtnis (rough translation: On Memory) and in this book he introduced the concepts of the forgetting curve and the spacing effect.

What is the forgetting curve and what does it measure?
One of Ebbinghaus’s goals was to find a relationship between our memories and time or in other words to figure out how low long does it take for us to forget what we learned. So in the simplest form, a forgetting curve is just a curve that tries to show a relationship between information retained (after you learn something) and time (that has elapsed after you learned something). And Ebbinghous wanted to figure out how did this curve looked like.
However, while measuring time is quite straightforward, measuring the amount of information retained is more complicated. So the first issue that Ebbinghaus faced was deciding what type of information should he memorize to conduct the experiment. After trying to memorize tones, numbers, and poem stanzas, he decided that trying to memorize random groups of nonsense syllables would be the best for his experiment. The other kinds of information were either too cumbersome to memorize (e.g. tones) or evoked too much meaning when memorizing and could introduce a measurement error (e.g. poems).
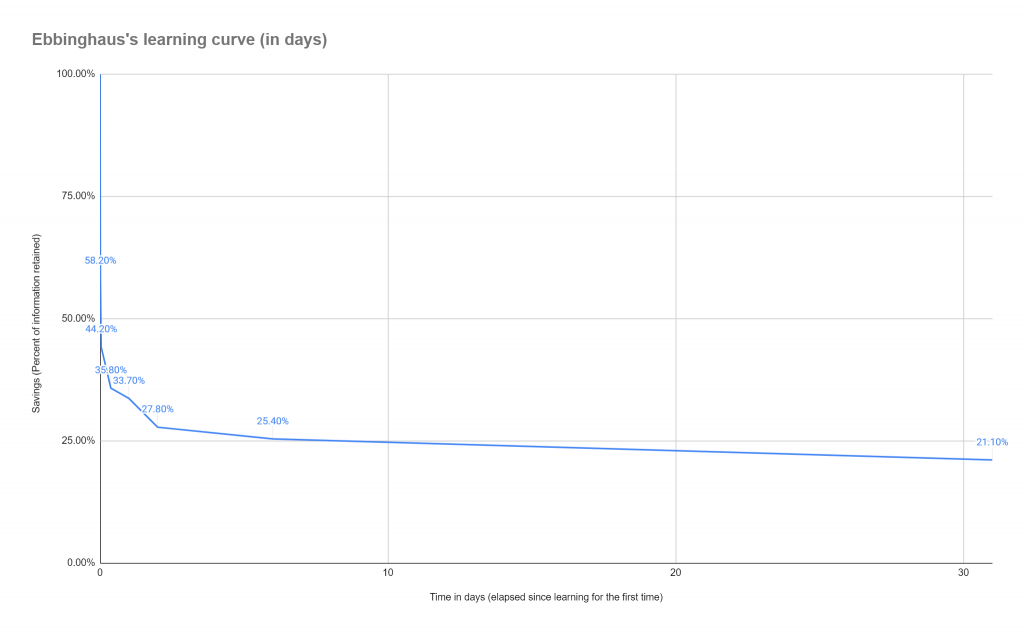
These nonsense syllables were single syllables consisting of 3 letters – 2 consonants and one vowel in the middle. For example RUR, HAL, MEK, BES, etc. In total, Ebbinghaus created about 2300 of these syllables. Then he created random lists of these syllables – each list consisting anywhere from 7 to 36 syllables (according to “How we learn” by Benedict Carrey) Then he began memorizing each of the lists and tracking the percentage of the list he remembered after a certain period of time – the periods of time that he used were 20 minutes, 1 hour, 9 hours, 1 day, 2 days, 6 days, 31 days. He took his results and plotted them on a curve – that is today known as the Ebbinghaus forgetting curve, which is the most widely known forgetting curve.
While in the table above the curve looks quite gradual – do not be deceived – this is so because the time axis is not spaced out in equal intervals. If you plotted the curve where the time axis would be only days this is how it would look like:
As evident from the curve, you will forget almost 70% of what you learn the first day. Of course, it is important to keep in mind that the aforementioned statement assumes that the results of the Ebbinghaus study can be generalized to other types of learning and to other people. However, as discussed further other scientists were able to replicate Ebbinghaus’s results.
How do you calculate forgetting curve?
To measure how much information he has retained after learning the list Ebbinghaus introduced a measure called Savings, which is defined as “the relative amount of time saved on the second learning trial as a result of having had the first”. And is calculated using the following formula:
(repetitions needed when learning for the first time – repetitions needed when learning for the second time )
_________________________________________________________________________________________________________
( repetitions needed when learning for the first time )
While the definition might sound rather complicated in practice it is quite simple. Let’s say to learn a list of 8 nonsense syllables Ebbinghaus had to repeat it 25 times. Then let’s say after 1 day, Ebbinghaus tries to repeat the same list again, but fails and needs to relearn it – this time he needs only 15 repetitions to relearn it. So his savings after 1 day are calculated as follows: (25-15)/25 = 0.4 = 40% – in this particular example the savings are 40 % which means that after 1 day Ebbinghaus retained 40% of the information he has learned. If you repeat the following procedure for different time intervals (e.g. 20 minutes, 1 hour, 9 hours, etc.) then you can collect enough data to plot your own forgetting curve.
Of course, doing this with just one list per each time interval might lead to biased results – maybe for some sort of reason you were able to memorize one list very easily because you were feeling well when memorizing it or this list for some sort of reason was just more memorable than others. To reduce such bias Ebbinghaus did this several times for each learning period and then took the average savings for each period.
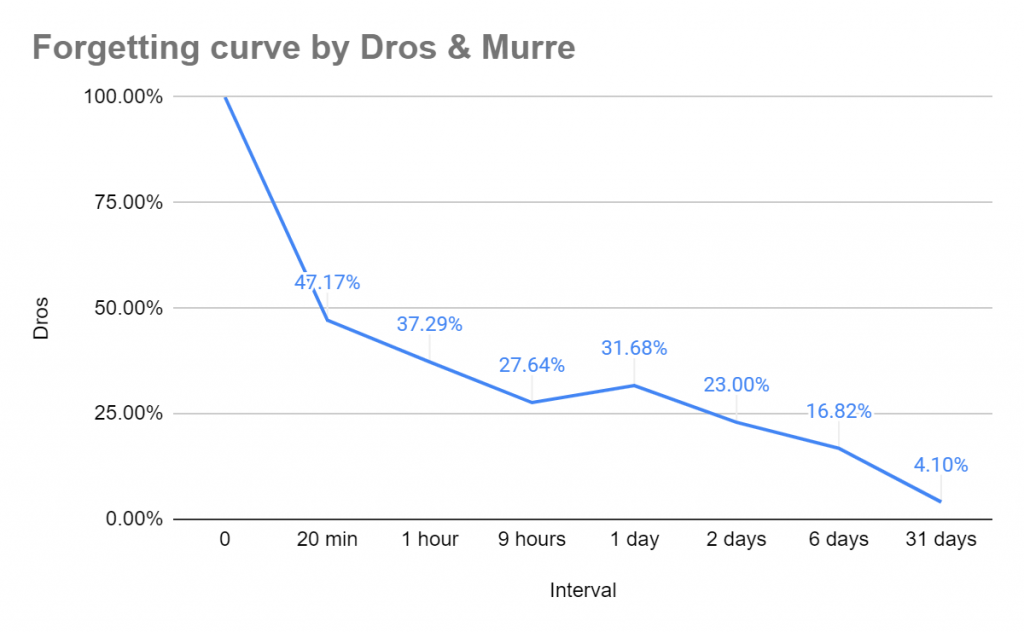
While I could not find the exact amount of lists Ebbinghaus used in his original study, here is how a similar study by Dros & Murre did it – they used 69 nine lists of nonsense syllables in total. They also used the same 7 time periods such as Ebbinghaus used – 20 minutes, 1 hour, 9 hours, 1 day, 2 days, 6 days, 31 days. To measure savings for each time period they used 10 lists per period (with the exception of the 9 hour period for which they used only 9 lists)
Here is the slightly simplified procedure that they followed for each period. They took a list of random syllables and calculated how many repetitions it took for their test subject to learn it e.g. 31 repetitions, then asked the test subject to wait the allotted time period – e.g. 1 day and then try to relearn the same list of the random syllables. After that was done they calculated how many repetitions it took for the person to relearn it e.g. 21 repetitions. Then they repeated the same procedure 9 more times with 9 different lists for the same 1 day period and averaged out the repetitions it took for the test subject to learn the list of syllables for the first time and how many repetitions it took for the test subject to relearn the lists after 1 day had elapsed.
The end result was that the average amount of repetitions the test subject needed to learn the list initially was 31.22 repetitions and then the average amount of repetitions they needed to learn the same syllable list after 1 day was 21.33 repetitions. Then they used this data to calculate the average savings percentage for a 1-day interval which in the case of Dros and Murre was (31.21-21.33)/31.22 = 31.7% They repeated the same procedure for each time period ( 20 minutes, 1 hour, 9 hours, 1 day, 2 days, 6 days, 31 days ) and they got the average savings numbers for these periods, which were used to plot the learning curve which can be seen below. You can use the same procedure to calculate a forgetting curve of your own, although this might be quite time-consuming and you might be better off just assuming that your learning curve will be quite similar to the one by Ebbinghaus or Dros. And if you read further you will see that this is a quite decent assumption.
What is the rate of the Forgetting Curve?
| Interval | Ebbinghaus | Mack | Seitz | Dros | Average |
| 20 min | 58.20% | 54.43% | 44.21% | 47.17% | 51.00% |
| 1 hour | 44.20% | 43.19% | 32.49% | 37.29% | 39.29% |
| 9 hours | 35.80% | 28.51% | 26.98% | 27.64% | 29.73% |
| 1 day | 33.70% | 31.60% | 27.00% | 31.68% | 31.00% |
| 2 days | 27.80% | 36.50% | 28.57% | 23.00% | 28.97% |
| 6 days | 25.40% | 30.89% | 20.52% | 16.82% | 23.41% |
| 31 days | 21.10% | 25.84% | 20.08% | 4.10% | 17.78% |
Joeri Dros
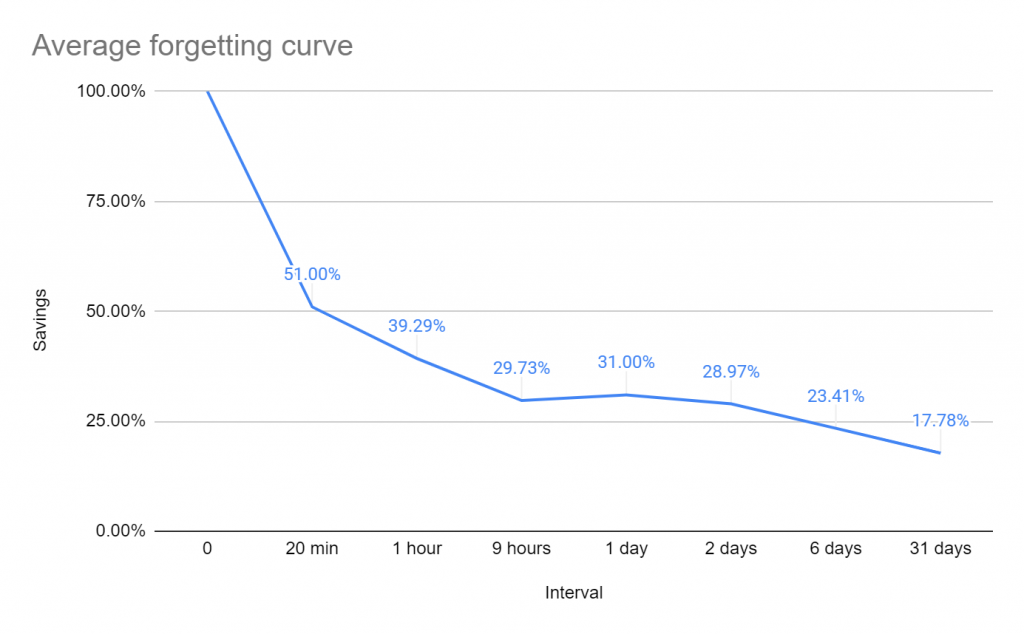
Many other scientists tried to replicate Ebbinghaus’s results and most of them found very similar forgetting curves. If you will take an average of the studies reviewed in a paper by Dros you will get the following rate of forgetting:
- In 20 mins people forget about 49% of the memorized nonsense syllables
- In 1 hour people forget about 61% of the memorized nonsense syllables
- In 9 hours people forget about 71%of the memorized nonsense syllables
- In 1 day people forget about 69%of the memorized nonsense syllables
- In 2 days people forget about 71% of the memorized nonsense syllables
- In 6 days people forget about 77% of the memorized nonsense syllables
- In 31 days people forget about 82% of the memorized nonsense syllables
If you plot the average forgetting curve this is what you will get:
Joeri Dros
It is quite interesting that there is a slight increase in savings on the 1-day interval when compared to the 9 hours interval. According to Murre and Dros, this might be due to the positive effects of sleep. This is quite interesting and in our article on studying vs sleep, we discuss this topic a bit more in-depth.
Concluding remarks
You should now have a pretty good understanding of the forgetting curve and how it is calculated. With that being said, there are limitations to it – the primary one being that this curve was created via the memorization of nonsense syllables. If one was to memorize a different kind of information the curve might differ. The main takeaway for me personally is that we do tend to forget most of what we learn almost immediately in about 1 day’s time. And the best way to combat this is via tests and spaced repetition.